Converting Altitude/Azimuth Coordinates to Equatorial

Probably the most daunting task in the entire Astronomy Before the Telescope Certification is the mathematical transformation needed to convert the Alt/Az angles of your measured stars into equatorial coordinates (RA/Dec) for plotting to make a Planisphere.  For Dob users there are a number of online calculators that can convert from equatorial to altitude/azimuth coordinate for use with Alt/Az setting circles.  Unfortunately for us, few if any online calculators can go the direction we need.  The process involves spherical trigonometry, radians, converting dates to Julian, and times to local sidereal.  Many might abandon the Certification because they would be turned off or simply lost at having to do the calculations.   One advantage of using the transit method for the measurements is that it simplifies the calculation a bit, but it is still difficult.  However, if you are a math/science type of person this calculation might be up your alley.  An introduction and suggestions for the mathematical approach can be found later in this document.

Readers may already have the free program Stellarium installed and should plan to use to it make the needed conversion.  While Stellarium wasn’t designed for the task, it can be used to quickly find approximate equatorial RA/Dec coordinates from Alt/Az data without the cumbersome math.  The error in the result is smaller than the ability to plot values so it should work for constructing a Planisphere.

Procedure:

1. Start Stellarium and configure the location of your observations by pressing Fn-F6 or moving the mouse to the left edge of the screen and selecting the Location button.  Either select your closest location from the list or enter the Latitude and Longitude information.  If needed, give your location a name and save.  Close the window.​
2. Select the time of your observation by pressing Fn-F5 or moving the mouse to the left edge of the screen and selecting the Date/Time button.  Make sure you select the Date and Time tab rather than Julian Date.   Set the time of your observation.  By default Stellarium updates in real time so you may want to freeze the time by pressing the J key on the keyboard.  Close the window.
3. Make sure you have the required information displayed on the upper left by pressing Fn-F2 or moving the mouse to the left edge of the screen and selecting the Configuration button.  In the new window select the Information tab and click the All available option.  If you wish to make it permanent select the Main tab where there is a Save Settings button.  If you wish to add fainter stars to Stellarium go to the Tools tab and click the Get Catalog button below Star Catalog Updates.  Close the window.
4. Now search for the position of your Alt/Az data.  Press Fn-F3, Ctrl-f, or move your mouse to the left edge of the screen and select the Search button.  This will bring up the Search window where you need to select the Position tab.  In this tab set the Coordinate System box to Horizontal and enter the azimuth and altitude data for your star.  As you enter the values the sky will move behind the window to find the location you have entered.  Close the Search window.
5. The last step is to zoom in on your location.  Pick a star that is close to the middle of the screen and click on it.  It may or may not be the star you actually measured.  Once you click on the star look at the information displayed on the left of the screen.  You should be able to see the Alt/Az coordinates on the star you clicked on and they should be fairly close to your measured values.  The equatorial coordinates (RA and Dec) are also displayed.  While they are not the true values for the location you measured because you clicked away from the real location, they should be very close and probably closer than your ability to put a point on a graph to represent them.

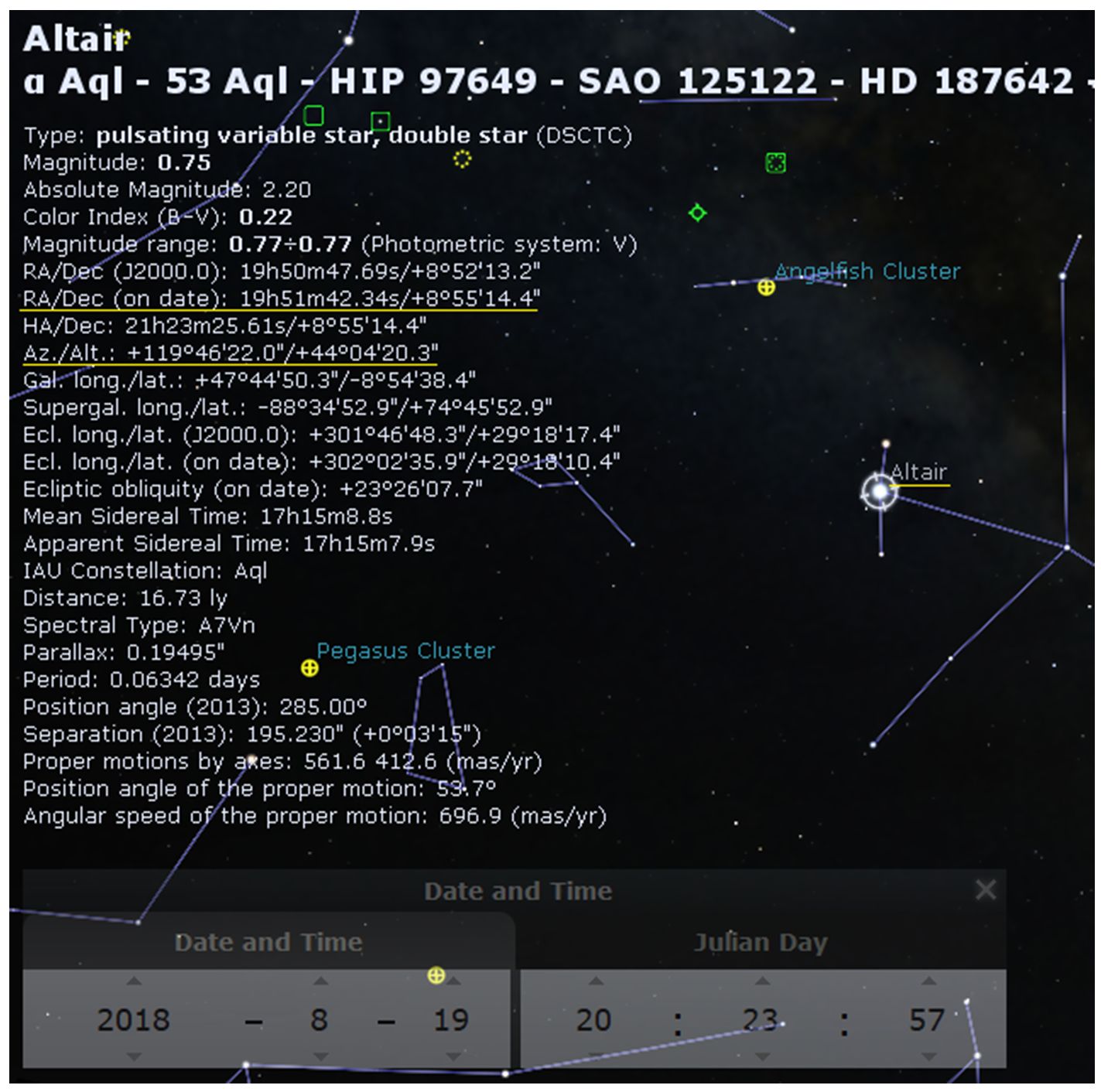
The picture below shows the process for Altair on 2018/8/19 20:23:57 from my location.  The Alt/Az and RA/Dec (JNOW) are underlined.

For Math Lovers

The conversion when the target is on the meridian:

You’ll need the measured altitude, the SIDEREAL TIME when the target is on the meridian, and your local latitude.  There are a number of programs that you can run while you are making your observations that display the sidereal time on the screen.   The secret here is that an object’s right ascension is the local sidereal time when it is on the meridian making R.A. trivial.  To find the declination from the altitude make use of:

sin(altitude) = sin(latitude)sin(declination) + cos(latitude)cos(declination)cos(local hour angle)

the local hour angle is 0 when an object is on the meridian.

Note that if you plan to do this with a spreadsheet many use radians as the default.

If the object isn’t on the meridian the basics of the actual mathematical transformation can be found on the Internet in a variety of sources.  One place to start is Positional Astronomy: Conversion between horizontal and equatorial systems. 

The best place to currently go (2018) is the book Practical Astronomy with your Calculator or Spreadsheet 4^th Edition by Peter Duffett-Smith and Jonathan Zwart.  The book is available on Amazon in a number of formats including rental.  The book has worked examples that show the needed steps to convert Alt/Az observations at a given time from a known location into equatorial RA/Dec coordinates.  If there is any downside it is that the book’s examples build on prior ones so to understand the conversion you need to work through a number of prior examples.  A balancing positive is that the book describes a number of “new” visual Basic functions for Excel or OpenOffice that aid all the needed calculations. The functions limited to use by the book’s owner and may not be presented here.  The book does not come with a CD, but all the worked examples are available via download at a URL found in the back.  Downloading the examples provides spreadsheets that contain the mentioned visual Basic functions.  The conversion from horizontal to equatorial coordinates makes use of seven of the seventy-five calculations described in the book.

For programmers with Python experience there are a number of astronomy related libraries that make the conversion fairly simple, particularly ephem or AstroPy.  Feel free to email the coordinator for more information if you are versed in Linux and/or Python.