Disclaimer
There are many assumptions and approximations in this process. Your results will vary depending on errors that creep into the process due to factors such as these:
- Planet orbits are elliptical, not circular
- Planets do not orbit in the same plane
- The Sun, Earth, and planet are seldom perfectly aligned
- We are ignoring effects from the Earth’s rotation
- We are ignoring any effects associated with the Earth’s orbital movement
- You are taking measurements from photos of extremely distant objects
Information on the Planetary Transit: Mercury 2019
The next planet to transit the sun is the planet Mercury on November 11, 2019. Details on transits are available from NASA on this site: http://eclipse.gsfc.nasa.gov/transit/transit.html. For information about this specific transit, click here.
Note that for many of us in the United States, the entire transit will not be visible. For those in the western United States, the transit will be already in progress at sunrise, so we will not be able to observe the entire event. Timings for the contacts are:
Event UT
- Contact I 12:35, November 11, 2019
- Contact II 12:37, November 11, 2019
- Maximum Transit 15:20, November 11, 2019
- Contact III 18:03, November 11, 2019
- Contact IV 18:04, November 11, 2019
Definition of contact points:
- Contact I: when the leading edge of the planet first touches the edge of the Sun.
- Contact II: when the planet is initially completely on the disk of the Sun.
- Maximum Transit: when the planet is at maximum transit (the middle).
- Contact III: when the leading edge of the planet first reaches the far edge of the Sun.
- Contact IV: when the planet is initially completely off the disk of the Sun.
Mercury is small and so far from Earth and its silhouette is visible only with magnification, but be sure to use proper filters to protect your eyes.
(The next transit after this one is the planet Mercury on November 13, 2032. Mark your calendar.)
How to Safely Observe the Transit
Observing the Sun can be very dangerous. Be very careful. Never look at the Sun without proper filters. A safe filter must filter 99.999% of the sunlight at visible as well as invisible wavelengths (infrared and ultraviolet). Damage can be immediate and permanent!
Option 1: Pinhole Projection. This is a great, low-tech way to watch the event. It lets multiple people see it at the same time. Do NOT look through the hole at the Sun. Put a small pinhole in the center of a card. Let the light coming through the hole hit a large white card or piece of paper about 3 feet away.
Option 2: Eyepiece Projection. This technique will work for a small telescope or a pair of binoculars mounted on a tripod. Do NOT look through the binoculars or the telescope when it is pointed near the sun! Do NOT do this with a large telescope, the optics may overheat and be permanently damaged. If you are using binoculars, cover one of the objective lenses. Point the equipment at the Sun. Then hold up a white card or piece of paper so that the light coming out of the eyepiece is projected onto the paper.
Option 3: Solar Sunglasses. Because of Mercury’s tiny angular diameter its disk will NOT be visible through Solar Sunglasses. These sunglasses are easily available on the internet and will be available in local stores as the time draws near. Once you have them, check to be sure that there is no damage. Put them on, and look at a bright incandescent light bulb. You should be able to see the glowing filament. Make sure that there are no cracks, creases, or pinholes. Even a small pinhole will let in a potentially dangerous amount of light from the Sun. It you see any damage at all, do NOT use them. Also note that there are NO sunglasses that are safe for looking at the sun.
Option 4: Binoculars or a Telescope with a Solar Filter. They should have a filter at the front end of them. Do NOT use solar filters that attach at the eyepiece end. Make sure that there is no damage on the filter before you use it. Be sure to cover the finder scope.
Option 5: A Solar Telescope. These are telescopes specifically designed for observing the sun usually at specific wavelengths (e.g. H-alpha – 656.3 nm, Calcium K – 393.4nm). I believe that the view in a standard telescope with a standard solar filter will be more pleasing.
Option 6: Shade #14 Welder’s Glass. Because of Mercury’s tiny angular diameter its disk will NOT be visible through Welder’s Glass. It is critical that you use shade #14 or higher. The higher number the more filtering. If you are unable to get the shade #14 welder’s glass, then we recommend that you use one of the projection methods (options 1 or 2 above). If you combine more than one piece, your total must be higher than 14. Two pieces should total 15. Three should total 16. If you use more than one piece, tape them together so that you will always be sure to be looking through all of the filtering. A higher number is always better.
Requirements to Receive Certification
You must be a member of the Astronomical League as a member of an astronomy club, or as a Member at Large to be eligible to receive this certification.
|
There are two options for this certification:
The observations required are:
|
*New* – An Alternative:
- We believe it may be possible to do the same calculations with any two well-spaced observations of the transit. It requires the additional step of determining the portion of the sun traversed between the two observations. You should be able to measure this from your images.
What we will attempt to calculate are:
- Oblateness of the Sun. (How flattened is the sphere?)
- Oblateness of the planet Mercury. (How flattened is the sphere?)
- Inclination of Mercury’s orbital plane,
- Mercury’s Orbital Period,
- Mercury’s velocity in its orbit,
- Answer a few thought questions,
There are many factors that must be taken into account to accurately calculate these values. We are going to make some simplifying assumptions to do these calculations based on the limited information our observations will collect. We know that these will have a significant impact the accuracy of our results.
Some of these assumptions are:
- We will assume that the Earth’s orbital path is a circle.
- The Earth’s distance from the sun, 1 A.U. will be assumed to be 149,600,000 km.
- We will assume that Mercury’s orbital path is a circle.
- Mercury’s distance from the sun, 0.4 A.U. will be assumed to be 57,910,000 km.
- Mercury’s axial tilt is 2.11°. We will assume it is 0°.
- We will ignore any effects of parallax caused by the observer’s location on Earth.
- We know that to be accurate on timing the length of the transit we can’t use first contact of Mercury on the Sun and last contact. Mercury has a diameter, and we should be using the center of Mercury crossing the edge of the solar disk.
A brief note on eccentricity (or ellipticity). Eccentricity is a measure of the degree to which an ellipse is not a perfect circle. These are the values of eccentricity for planet shapes or orbits:
- e = 0: circle Eccentricity can be calculated using this formula:
- 0 < e < 1: ellipse e = (ra – rp) / (ra + rp)
- e = 1: parabola ra is the most distant point in the orbit (apoapsis)
- e > 1: hyperbola rp is the closet point in the orbit (preiapsis)
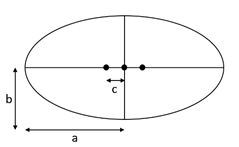
Note: For planet shapes we look at oblateness, but the concept is very similar. The flattening (f) can be calculated using this formula: f = (a – b) / a where is the equatorial diameter and b is the polar diameter.
Required Activities
Step 1: Calculate the oblateness of the Sun: based on the full-disk image of the Sun
- Note: You must consider the type of telescope and mount that you are using. An altitude/azimuth mount will experience field rotation during the duration of the transit. This must be included in your analysis. Based on your type of telescope and mount, you should be able to determine the orientation of the Sun.
- Note: There is a great tool that has been developed by Les Cowley called TiltingSun. It will help you determine the precise orientation of the sun’s axis based on your date, time, telescope, and mount. It can be downloaded free from his website (click here). The on-line instructions are well done and very useful. They can also be downloaded as a PDF file here. This will confirm your estimate in Step 1. Use this information for successive calculations.
- Based on your photographic setup or the data from TiltingSun you should be able to determine the orientation of the Sun.
- NASA has calculated the Sun’s axial tilt at 7.25°. The sun’s north pole is pointed at the Earth in September.
- If the Earth’s orbit were truly a circle, then we move 30° per month.
- The Sun’s axial tilt (x) will appear as: x = 7.25 * sin(60°).
- Calculate the Sun’s apparent axial tilt for November.
- Identify the north pole of the Sun. Since the Earth orbits in a counterclockwise direction, the axis will move from vertical in a counterclockwise direction on the face of the Sun.
- Based on the north-south orientation of the Sun, measure the polar diameter of the Sun in the north-south direction.
- Measure the equatorial diameter of the Sun in the East-West direction.
- Theory predicts that rotating spheres will bulge around the equator and not be spheres but will be oblate spheroids. Calculate the oblateness of the sun based on these two values.
- e = c / a: e is oblateness, c is the distance from center to either focal point, and a is the length of the Semi-Major Axis.
- c can be calculated using this formula: c2 = a2 – b2 where b is the length of the Semi-Minor Axis.
- And substituting for c, you get: e = sqrt((a2 – b2) / a).
Step 2: Calculate the oblateness of the planet Mercury: based on the full disk image of Mercury
- NASA has calculated Mercury’s axial tilt at 2.11°. We will use 0° for this value.
- Repeat the process in Step 1 using the image of Mercury to calculate the eccentricity of the planet Mercury.
Step 3: Calculate the inclination of Mercury’s orbital path
- Record the time and location of Mercury’s ingress onto the Sun.
- Record the time and location of Mercury’s egress from the Sun.
- Draw the line of the transit on the Sun and compare it to the east-west line.
- Determine the inclination of Mercury’s orbit. Inclination is the angle between these two lines.
- Note: If the transit occurred at the point where Mercury, the Sun, and the Earth were perfectly aligned, then the path of the transit would pass directly through the center of the solar disk. This is a rare event.
Step 4: Calculate Mercury’s Orbital Period
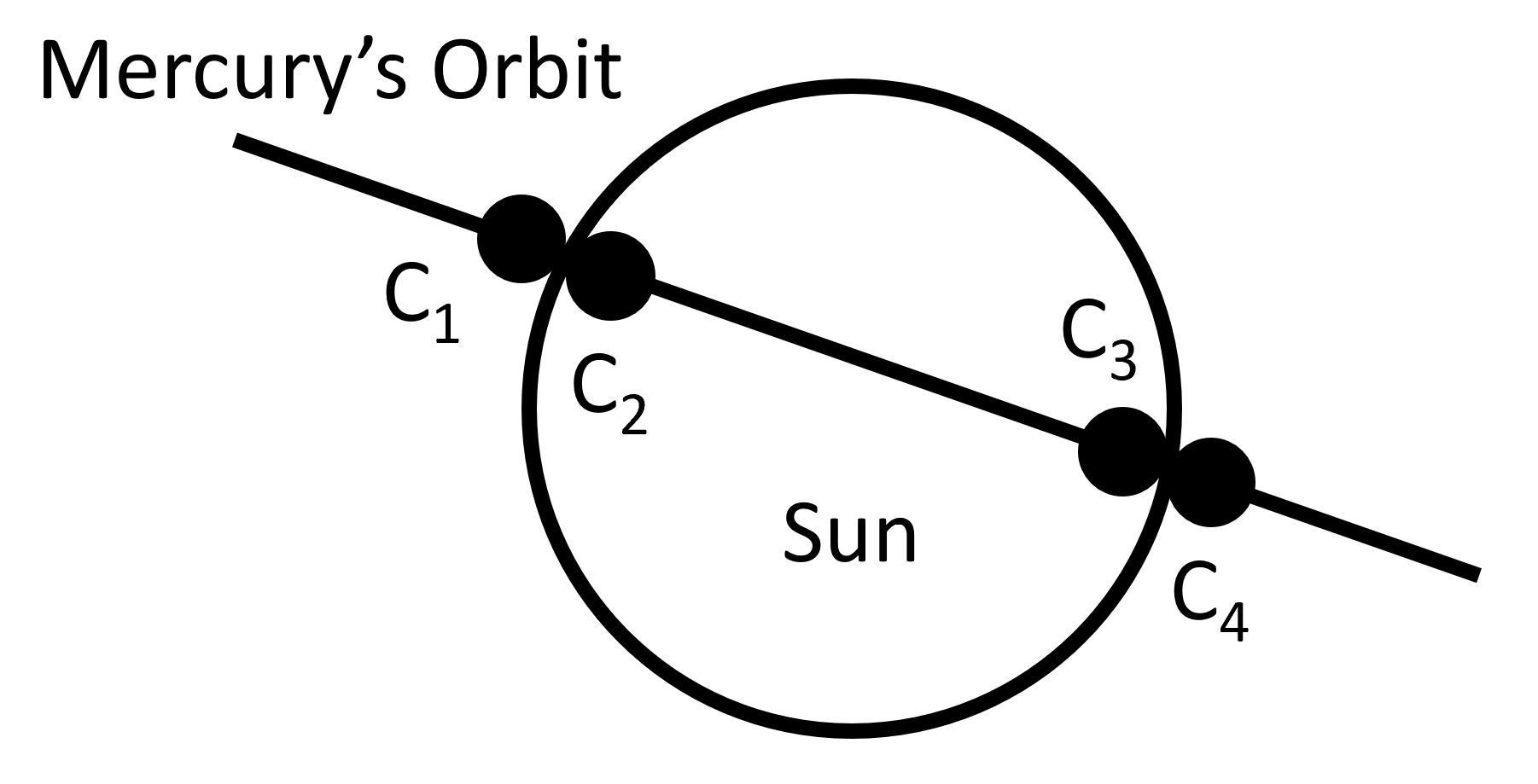
- Mercury will be very tiny. It is very difficult to note the time of first contact (C1) and last contact (C4). We will use the points where Mercury is first completely on the Sun (C2) and where it is last compeltely on the Sun (C3) Based on these times of ingress (ti) and egress (te) of Mercury, calculate the duration of the transit (tt in minutes). The equation is: tt = te – ti.
- Note: This is missing the time it takes for one diameter of Mercury to be crossed. According to NASA, for this transit, this is 1:41 (1.68 minutes). Add this to tt to be a bit more accurate.
- It would be very difficult to calculate the orbital period (T) from the transit, so we will fall back on Kepler’s Third Law of planetary motion. This law says that the Orbital Period (in years) can be calculated if you know the semi-major axis (in A.U.s). Mercury’s semi-major axis (a) can be assumed to be 0.387 A.U. Kepler’s Third Law states: T2 = a3. So T = sqrt(a3). Calculate the value for the Period (in years).
- Convert this to days. You can use 365.25 days per year.
Step 5: Calculate Mercury’s velocity in orbit
- Compute the length of Mercury’s orbit (in kilometers) based on Mercury’s semi-major axis (rm = 0.387 A.U., the A.U. is 149,600,000 km). lo (length or orbit in km) = 2 * pi * rm = 2 * pi * 0.387 (in A.U.) * 149,600,000 (km per A.U.)
- Based on this and the orbital period for the orbit, calculate the average speed of Mercury in its orbit. vm = lo / to.
- Note: Mercury’s orbit is in an ellipse, not a circle. We know from Kepler’s Second Law of planetary motion that when a body is orbiting in an ellipse, that objects speed changes as it orbits; going fastest when at perihelion, and slowest when at aphelion. We made this simplifying assumption since we are not sure where Mercury is in its orbit at the time of the transit.
Step 6: Some questions to be answered
- Why do you think The Sun would have such a small oblateness?
- Why do you think the planet Mercury would have such a small oblateness?
- Of the assumptions that we made, which one do you think caused the largest error in the calculations of Mercury’s orbital period?
- What might be the cause for error in calculating Mercury’s orbital inclination?
Submitting Your Results to the AL Coordinator
The Coordinator must receive submissions for this program no later than December 11, 2019. There will be no exceptions. A certificate and a pin will be awarded to those Astronomical League members who participate.
|
Information Required:
|
Planetary Transit Special Award Coordinator:



